An introduction to adaptive numerical methods

In collaboration with my friend and colleague Ben Couchman, I'm embarking on a series of blog posts that explain what it is exactly that I am getting a Ph.D. for studying. Please enjoy.

Computational Fluid Dynamics

The top line answer to: "what do you do?" is simple. At it's most simple, my job is to simulate fluid flows. When I say fluid, I mean either liquid or gas. But I pretty much mean one gas in particular: air. Airflow is important to a lot of things. In my home discipline, Aerospace Engineering, it's rather important for keeping planes in the sky. So a typical result of a Computational Fluid Dynamics– CFD for short– simulation for an aircraft might look like this:

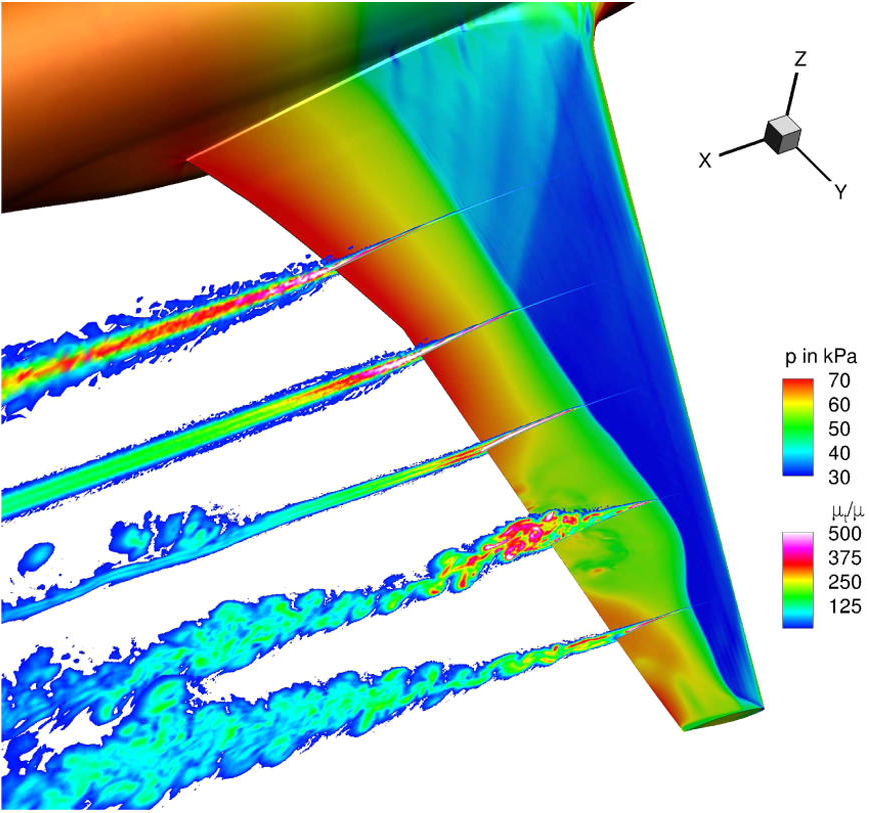
The flow of air around an aircraft, as it turns out, it complicated and costly to simulate. CFD endeavors to take on that task, and my work in particular seeks to reduce the cost of doing so for the most expensive types of simulation.

An example of this sort of problem that lies outside the traditional scope of aerospace is found in wind energy. Approximating the extractible energy in a future wind farm, it turns out, is very hard to do. At the same time, placing each wind turbine at just the right place on the farm can drastically improve the ability of the wind farm to extract the available energy. CFD simulations like the one below, from research led by researchers at Johns Hopkins University, make it possible to project what the extraction capability of an unbuilt wind farm might be.

Ok, so what's so hard about that?

Think about smoke rising from a candle that was just blown out. There's an extinguished but hot wick, which is dumping smoke that makes the airflow visible. The smoke makes it clear that the air that is heated by the wick rises, in a column, while the air around it rests. As it rises it mixes with the rest of the air in a chaotic and unpredictable way, until it's virtually indistinguishable from the rest of the air around it.

If we were to attempt to simulate this perfectly we would have to simulate every tiny constituent particle of the air. It turns out that there's ... well ... too many of these to do that. Thanks to brilliant work from a long sequence of generations of good mathematicians, scientists, and engineers, we have a way of representing these things that is much more managable. But nonetheless, we have to account for every meaningfully significant motion that occurs in all of the three dimensional space of the room that the candle is in. Even if we don't have to simulate every single particle, this is a ton of information.

We use the idea of a "grid" or a "mesh" to represent the discrete and finite representation of all of this information about the flow. If we were taking a digital photograph, the "grid" or "mesh" would be like the empty data structure that comes from the camera's sensor, like a bunch of empty spaces that we are planning to put pixels. They look something like this:

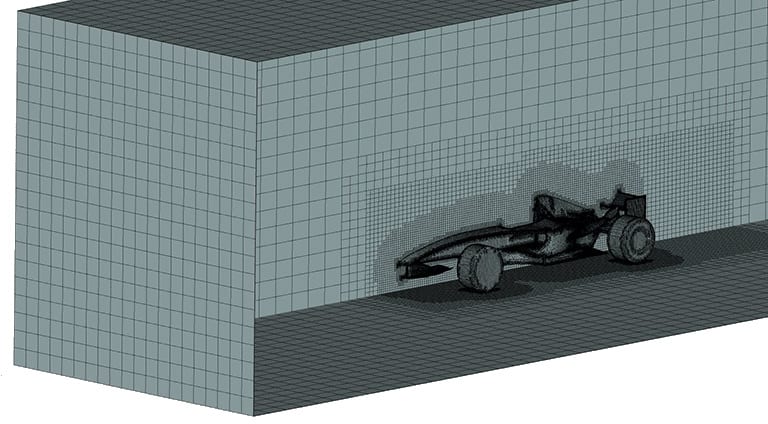
You may notice now that this is different than a camera in that it isn't a nice and uniform grid, but one that is catered to the problem of interest. In that way you would be 100% correct. In the industry right now, people spend a lot of time deciding where exactly to put the simulation equivalent of pixels, which, in CFD simulations like the ones used in my work, are called "elements". The problem with this, it turns out, is that having a human decide where to put the pixels can really effect how clear the image ends up being. In fact, the analogy breaks down for physical simulations and makes matters even worse; unlike in a photograph, a simulation's accuracy at one point depends on the accuracy at other points in the domain (analogous to the "frame" of the photograph) and even how accurate the simulation was in the previous frame.

The million-dollar question: can we figure out a way to do simulations better (and more efficiently) in an automated way?

Thus, we arrive at the key question: can we automate the process of putting the elements in the right places at the right sizes so that they most accurately represent the motion of a flow? If you follow the photograph analogy, for example, then the question is basically is there something like data compression that we can do to maximize the storage of information about the flow on the grid? This is the fundamental research question. The answer, which Ben and I will expound on in a series of posts is: yes, but it is not easy. However, our research and the research of lots of other people is attempting to show that it can be worth it.
In a series of posts, which will be linked here as they become available, we will try to show how we can:

• write the equations of motion for a flow in a way that makes automatically solving complex flows practical
• solve for these equations to approximate a flowfield and for quantities of interest of a flow
• figure out a way to approximate the effect of changing the grid on quantities of interest
• use this information to approximate the error in a simulation for a given grid configuration
• reconfigure the grid to decrease the error in the simulation
• ???
• profit